Critical Task

Table of Contents

1. Overview
2. Role
3. Problem
4. Goal
5. Solution

Overview

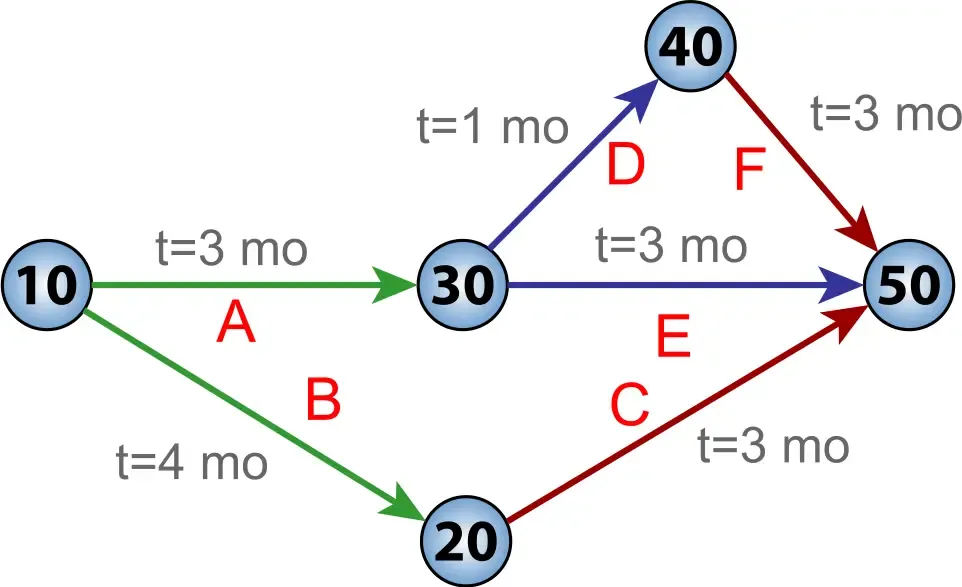
A topological sorting-based solution for project scheduling using directed acyclic graphs (DAGs). Implements PERT/CPM methodologies to calculate:

• Earliest start/finish times (forward pass)
• Latest start/finish times (backward pass)
• Total float/slack time

For more reading: PERT

👨‍💻 Role

Lead Developer

❓ Problem

1. Task dependencies created non-trivial scheduling constraints
2. Manual critical path identification proved error-prone for large projects (n > 100 tasks)
3. Schedule not optimally formatted in relation to time effeciency.

🎯 Goal

1. Develop O(n) algorithm for critical path identification
2. Model both AND/OR task dependencies
3. Achieve 95% accuracy vs. ground truth schedules

✨ Solution

Graph Representation

• Designed adjacency list structure with edge weights for task durations
• Implemented topological sort using Kahn’s algorithm (indegree counting)

PERT Implementation

• Calculated expected time for stochastic tasks
• Performed forward/backward passes with memoization for O(n) efficiency

Critical Path Analysis

• Identified zero-slack tasks constituting critical path
• Determine optimal task to perform